검색결과 리스트
글
신경망 이론
1. 신경망의 분류
현재 다양한 신경망 모델들이 제안되고 있지만, 다음과 같이 몇가지 기준에 따라 신경망을 분류할 수 있다.
1. 계층수 : 단층 구조, 다층 구조
2. 출력 형태 : 순방향 구조, 순환 (궤환) 구조
3. 데이터 유형 : 디지털, 아날로그
4. 학습 방법 : 지도 학습, 자율학습, 경쟁식
5. 활성화 함수 : 단극성, 양극성
신경망은 일반적으로 계층의 수에 따라 크게 단층 신경망과 다층 신경망의 2 가지로 구분된다.
단층 (single-layer) 신경망은 가장 단순한 구조로서 그림 1 에 도시한 바와 같이 외부 입력을 받아들이는 입력층 (input layer) X 와 신경망에서 처리된 결과를 출력하는 출력층 (output layer) Y 로 구성된다.
단층 신경망의 출력 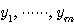 은 다음과 같다.
은 다음과 같다.
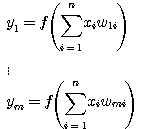
여기서, 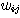 는 입력층 뉴런
는 입력층 뉴런  와 출력층 뉴런
와 출력층 뉴런 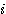 간의 연결강도이다.
간의 연결강도이다.
다층 (multi-layer) 신경망은 여러 계층으로 구성된 신경망 구조이다. 일반적으로 가장 널리 사용되는 것은 3 계층 신경망 구조이며, 그 구조는 그림 2 에 도시한 바와 같다. 3 계층 신경망은 외부 입력을 받아들이는 입력층, 처리된 결과가 출력되는 출력층, 입력층과 출력층 사이에 위치하여 외부로 나타나지 않는 은닉층 (hidden layer) 의 3 계층으로 구성되어 있다.
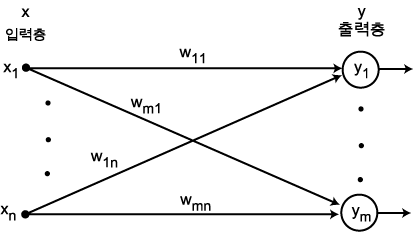
그림 1 단층 신경망의 구조
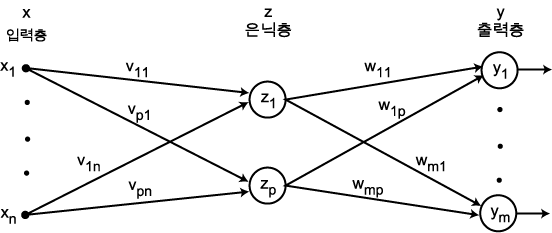
그림 2 다층 신경망의 구조
3 계층 신경망 구조에서는 입력층의 입력에 따라 은닉층의 출력이 나오며, 은닉층의 출력은 다시 출력층에 입력되어 최종 출력이 나오게 된다.
은닉층의 출력 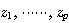 는 단층 신경망의 경우와 마찬가지로 다음과 같이 구할 수 있다.
는 단층 신경망의 경우와 마찬가지로 다음과 같이 구할 수 있다.
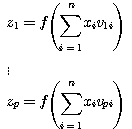
여기서, 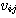 는 입력층 뉴런
는 입력층 뉴런  와 은닉층 뉴런
와 은닉층 뉴런 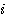 간의 연결강도이다.
간의 연결강도이다.
따라서, 최종 출력 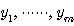 은 다음과 같다.
은 다음과 같다.
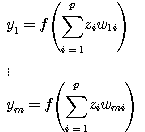
여기서, 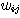 는 은닉층 뉴런
는 은닉층 뉴런  와 출력층 뉴런
와 출력층 뉴런 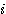 간의 연결강도이다.
간의 연결강도이다.
일반적으로 3 계층 신경망 구조가 널리 사용되지만, 특수한 응용 목적에 따라서는 2 개 또는 3 개의 은닉층을 사용하는 4 계층 또는 5 계층의 다층 신경망 구조도 이동되고 있다.
단층 신경망은 그림 3 (a) 에 도시한 바와 같이 AND, OR 연산 등 선형 분리 가능한 응용에만 적용할 수 있으나, 다층 신경망은 (b) 에 도시한 바와 같이 임의 유형의 분류가 가능하므로 보다 다양하게 응용될 수 있다.
또한, 신경망의 출력 형태에 따라서는 순방향 신경망 구조와 순환 신경망 구조의 2 가지로 구분할 수 있다.
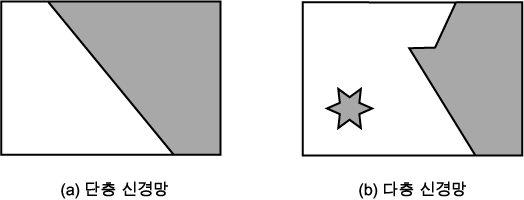
그림 3 신경망 구조에 따른 기능
순방향 신경망 (forward network) 구조는 그림 4 (a) 에 도시한 바와 같이 신경망의 출력은 단지 입력에만 관련된다. 예를 들어, 그림 4 (b) 와 같은 순방향 구조의 단층 신경망의 출력 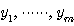 은 다음과 같다.
은 다음과 같다.
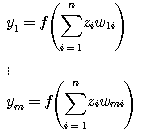
순환 신경망 (recurrent network) 구조는 그림 5 (a) 에 도시한 바와 같이 신경망의 출력이 다시 입력측에 궤환되어 새로운 출력이 나오는 형태이다. 예를 들어, 그림 5 (b) 와 같은 순환 구조의 단층 신경망의 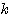 번째 출력
번째 출력 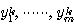 은 다음과 같이 구할 수 있다.
은 다음과 같이 구할 수 있다.
첫 번째 출력 :
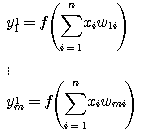
ㆍ
ㆍ
ㆍ
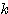 번째 출력 :
번째 출력 :
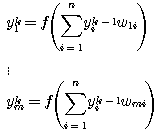
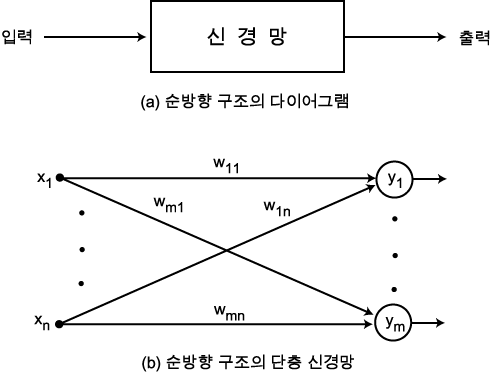
그림 4 순방향 신경망
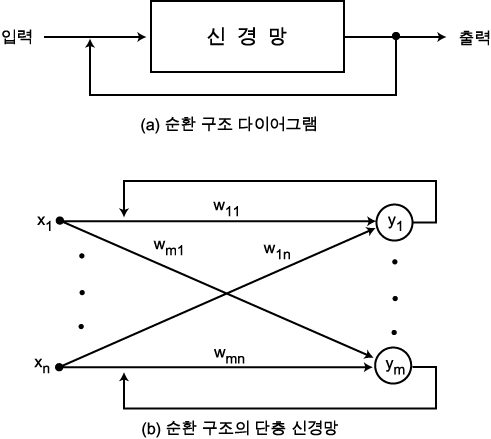
그림 5 순환 신경망
또한, 신경망에 입력되는 데이터의 유형에 따라서는 디지털 신경망과 아날로그 신경망으로 구분된다. 학습 방법에 따라서는 지도학습과 자율학습으로 구분되며, 활성화 함수에 따라서는 단극성 및 양극성으로 구분된다. 활성화 함수와 학습 방법에 대해서는 활성화 함수와 신경망의 학습에서 자세히 언급하기로 한다.
그림 6 은 입력 데이터 및 학습 방법에 따라 신경망을 분류한 것이고, 표 1 은 다양한 응용분야에 따라 주로 활용되는 신경망 모델을 분류한 것이다.
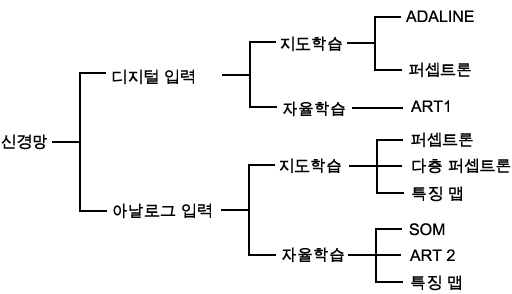
그림 6 입력 데이터 및 학습 방법에 따른 신경망의 분류
표 1 응용 분야에 따른 신경망 모델의 분류
응 용 | 신경망 유형 |
패턴 분류 | ADALINE ART Boltzmann Machine Feature Map Hamming Net Multilayer Perceptron |
음성 인식 | Multilayer Perceptron Silicon Cochlea Time-Delay Net Viterbi Net |
영상 인식 | Cellular Automata Connectionist Model Neocognitron Silicon Retina |
로봇 제어 | CMAC Cerebellum Model Multilayer Perceptron Topographic Map |
연상 메모리 | Hopfield Model Bidirectional Associative Memory |
신호 처리 | MADALINE Multilayer Perceptron |
최적화 및 근사계산 | Boltzmann Machine Cellular Automata Counterpropagation Net Hopfield Model Winner-Take-All Net |
2. 벡터
신경망에 있어서는 입출력이 벡터 형태이고, 연결강도가 벡터 또는 행렬형태이므로 벡터 및 행렬의 연산이 필수적으로 요구된다. 본 절에서는 먼저 신경망 이론 전개에 필요한 벡터의 특성에 대하여 알아 본다.
우리가 일상적으로 접하는 시간, 온도, 길이, 질량 등 크기만으로 표현할 수 있는 물리량은 스칼라이다. 이에 비하여 힘, 변위, 속도 등 크기와 방향으로 표현하여야 하는 물리량을 벡터 (vector) 라 한다. 이와 같이 2 가지 요소에 의해 표현될 수 있는 벡터는 그림 1 에 도시한 바와 같이 2 차원 공간에서 시점과 종점을 연결하는 방향성 선분으로써 기하학적으로 표현할 수 있으며, 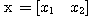 로 표기한다.
로 표기한다.
마찬가지로, n 개의 요소에 의해서 특성이 결정되는 벡터 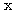 는 다음과 같이 표기할 수 있다.
는 다음과 같이 표기할 수 있다.
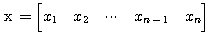 (1)
(1)
여기서, 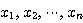 을 벡터
을 벡터 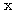 의 구성 요소 (component) 라 하며, 구성 요소의 개수 n 을 벡터의 차원 (dimension) 이라고 한다.
의 구성 요소 (component) 라 하며, 구성 요소의 개수 n 을 벡터의 차원 (dimension) 이라고 한다.
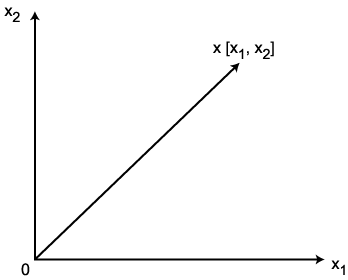
그림 1 벡터의 기하학적 표현
또한, 식 (1) 과 같이 표현한 벡터를 열벡터 (row vector) 라 하며, 식 (2) 와 같이 표현한 벡터를 행벡터 (column vector) 라고 한다.
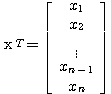 (2)
(2)
n 차원의 두 벡터 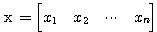 ,
, 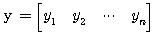 에 대하여 다음의 연산이 성립한다.
에 대하여 다음의 연산이 성립한다.
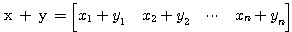
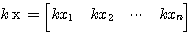
또한, 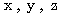 를 벡터라 하고,
를 벡터라 하고, 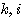 을 스칼라라 하면 다음과 같은 벡터 연산이 성립한다.
을 스칼라라 하면 다음과 같은 벡터 연산이 성립한다.
1. x + y = y + x
2. (x + y) + z = x + (y + z)
3. x + 0 = x
4. x + (-x) = 0
5. 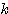 (
(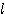 x) = (
x) = (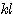 ) x
) x
6. 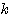 (x + y) =
(x + y) = 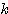 x +
x + 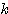 x
x
7. (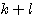 ) x =
) x = 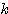 x +
x + 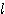 x
x
8. 1 x = x
예제 1 두 벡터 x = [1 2], y = [3 4] 가 있다. 2 x + y 는? 2 x = 2[1 2] = [2 4] 이므로 2 x + y = [2 4] + [3 4] = [5 8] |
한편, n 차원 벡터 x 의 길이 (norm), 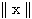 는 다음과 같이 구할 수 있다.
는 다음과 같이 구할 수 있다.
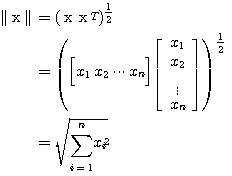 (3)
(3)
예제 2 x = [1 2 1] 의 norm 을 구하여라. x 의 norm 은 식 (3) 에 의하여,
|
이제, 벡터의 선형 독립성 (linearly independence) 에 대하여 알아 본다. 다음과 같이 벡터 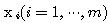 들의 선형 결합인 벡터
들의 선형 결합인 벡터 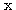 가 있을 때
가 있을 때
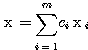
여기서, 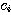 는 스칼라이다. 만약,
는 스칼라이다. 만약, 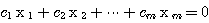 를 만족하는 모두 0 이 아닌
를 만족하는 모두 0 이 아닌 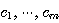 존재하면
존재하면 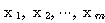 의 벡터 집합을 선형 종속이라하며, 그렇지 않으면 선형 독립이라 한다.
의 벡터 집합을 선형 종속이라하며, 그렇지 않으면 선형 독립이라 한다.
예제 3 다음 벡터는 선형 독립인가? (a) (b) (a) (b) |
일반적으로 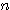 개의 입력을 받아 하나의 출력이 나가는 신경망의 경우에는 입력뿐만 아니라 연결강도도 역시 벡터 형태가 되므로 출력 뉴런의 NET 값을 구하기 위해서는 벡터의 곱셈이 요구된다.
개의 입력을 받아 하나의 출력이 나가는 신경망의 경우에는 입력뿐만 아니라 연결강도도 역시 벡터 형태가 되므로 출력 뉴런의 NET 값을 구하기 위해서는 벡터의 곱셈이 요구된다.
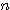 차원의 두 벡터
차원의 두 벡터 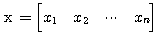 ,
, 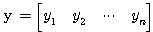 의 내적 (inner product) 은 다음과 같이 정의되며, 그 결과는 스칼라이다.
의 내적 (inner product) 은 다음과 같이 정의되며, 그 결과는 스칼라이다.
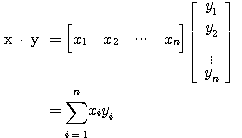 (4)
(4)
예제 4 x = [1 2 3], y = [1 0.5 1] 의 내적은?
|
특히, 연상 메모리의 용량에는 저장되는 패턴 벡터들간의 직교성이 상당한 영향을 미치므로 벡터의 직교성에 대하여도 알아 둘 필요가 있다.
만약, 식 (4) 와 같이 구한 내적이 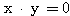 이면 두 벡터
이면 두 벡터 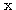 와
와 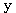 는 서로 직교 (orthogonal) 한다고 하며,
는 서로 직교 (orthogonal) 한다고 하며, 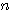 개의 0 이 아닌 벡터
개의 0 이 아닌 벡터 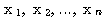 이 서로 직교하면 이 벡터들의 집합은 선형 독립이다.
이 서로 직교하면 이 벡터들의 집합은 선형 독립이다.
예제 5 다음과 같은 두 벡터 x = [1 0] y = [0 1]
따라서, 내적이 0 이므로 벡터
|
3. 매트릭스
단층 구조의 신경망에서 출력층의 뉴런이 다수이거나 다층 구조의 신경망에서 은닉층 및 출력층의 뉴런이 다수일 경우에는 연결강도가 행렬 형태가 되므로 행렬의 연산이 불가피하다. 본 절에서는 신경망 이론 전개에 필요한 행렬 (matrix) 의 특성에 대하여 알아본다.
숫자들의 사각형 배열을 행렬이라 정의하며, 배열내의 숫자들을 원소 (element) 라 한다. 일반적으로 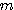 개의 열 (row) 과
개의 열 (row) 과 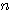 개의 행 (column) 으로 구성된 배열을
개의 행 (column) 으로 구성된 배열을 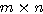 행렬라 한다.
행렬라 한다.
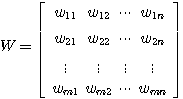 (1)
(1)
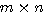 행렬 W 에서
행렬 W 에서 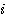 번째 열과
번째 열과  번째 행은 다음과 같으므로 열벡터는
번째 행은 다음과 같으므로 열벡터는 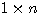 행렬
행렬 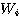 , 행벡터는
, 행벡터는 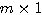 행렬
행렬 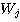 로 간주할 수 있다.
로 간주할 수 있다.
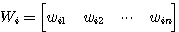
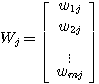
한편, 식 (1) 에서 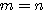 이면 정방형 (square) 행렬이라 한다. 행렬의 행과 열의 원소를 교환하여 생성된 것을 치환 (transposition) 행렬라 하고,
이면 정방형 (square) 행렬이라 한다. 행렬의 행과 열의 원소를 교환하여 생성된 것을 치환 (transposition) 행렬라 하고, 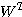 라 표현하며, 만약,
라 표현하며, 만약, 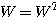 이면 대칭 (symmetric) 행렬이라 한다.
이면 대칭 (symmetric) 행렬이라 한다.
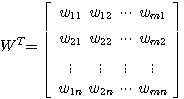
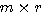 행렬 X 와
행렬 X 와 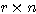 행렬 W 를 곱하면 그 결과는 다음과 같이
행렬 W 를 곱하면 그 결과는 다음과 같이 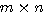 행렬이 된다.
행렬이 된다.
▲ ▲ = ▲ ▲ | |||||
|
|
|
|
|
|
|
|
|
|
|
|
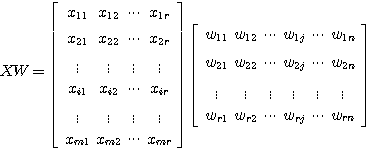
XW 의 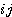 번째 원소는 다음과 같다.
번째 원소는 다음과 같다.
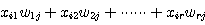 (2)
(2)
예제 1 다음 두 행렬을 곱하라. (a) (b) (a) (b)
(b) 의 경우에는 행렬 X 와 W 는 서로 곱할 수 없으나
| ||||||||||||||||||||||||||||||||||||
또한, 연상 메모리에서 저장 용량과 밀접한 관계가 있는 고유벡터 (eigenvector) 및 고유값 (eigenvalue) 에 대하여도 알아둘 필요가 있다.
만약, 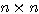 행렬 W 에 대하여 다음 조건을 만족하는 0 이 아닌 벡터
행렬 W 에 대하여 다음 조건을 만족하는 0 이 아닌 벡터 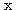 가 존재할 때
가 존재할 때 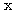 를 고유벡터라 하며, 스칼라 λ 를 행렬 W 의 고유값이라 한다.
를 고유벡터라 하며, 스칼라 λ 를 행렬 W 의 고유값이라 한다.
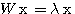 (3)
(3)
예제 2 행렬 식 (3) 에 의하여,
λ 가 고유값이면 0 이 아닌 해를 가져야 하므로,
즉,
따라서, W 의 고유값은 |
4. 활성화 함수
인공 신경망 모델에서 뉴런의 주요 기능은 입력과 연결 강도의 가중합 NET 를 구한 다음 활성화 함수에 의해 출력을 내보내는 것이다. 따라서, 어떤 활성화 함수를 선택하느냐에 따라 뉴런의 출력이 달라질 수도 있다.
활성화 함수 (activation function) 는 단조 증가하는 함수이어야 하며, 일반적으로 다음과 같이 분류할 수 있다. 이들 분류 방법은 서로 연관되어 있기 때문에 엄밀히 구분하여 설명하기 보다는 독자의 이해를 돕기 위하여 일반적으로 사용되는 함수를 위주로 기술한다.
1. 단극성 (unipolar) / 양극성 (bipolar) 함수
2. 선형 (linear) / 비선형 (nonlinear) 함수
3. 연속 (continuous) / 이진 (binary) 함수
4.1 항등 함수
항등 함수 (identity function) 는 그림 1 에 도시한 바와 같이 양극성이며, 선형 연속 함수이다. 항등 함수를 수학적으로 표현하면 다음과 같다. 따라서, 항등 함수를 활성화 함수로 사용하면 뉴런의 NET 즉, 입력의 가중합이 그대로 출력된다.
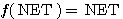 (1)
(1)
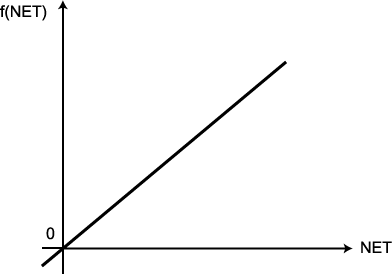
그림 1 항등함수
예제 1 다음과 같은 신경망 모델에서 그림 1 과 같은 항등 함수를 활성화 함수로 사용할 경우, 뉴런의 출력은?
입력 벡터 NET = 따라서, 뉴런의 출력은 식 (1) 에 의해,
|
4.2 경사 함수
경사 함수 (ramp function) 는 그림 2 에 도시한 바와 같이 단극성이며, 선형 연속 함수이다. 경사 함수를 수학적으로 표현하면 다음과 같다.
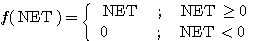 (2)
(2)
따라서, 경사 함수를 활성화 함수로 사용하면 NET 값이 0 보다 적을 경우에는 뉴런의 출력이 0 이지만, NET 값이 0 보다 크거나 같은 경우에는 항등 함수와 마찬가지로 NET 값이 그대로 출력된다.
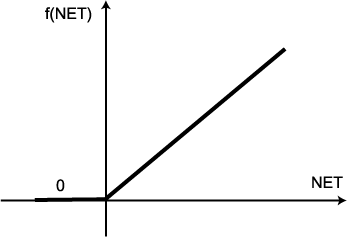
예제 2 다음과 같은 신경망 모델에서 그림 2 와 같은 경사 함수를 활성화 함수로 사용할 경우, 뉴런의 출력은?
입력 벡터 NET = 따라서, 뉴런의 출력은 식 (2) 에 의해,
|
4.3 계단 함수
계단 함수 (step function) 는 그림 3 에 도시한 바와 같이 단극성 또는 양극성 이진 함수이며, 디지털 형태의 출력이 요구되는 경우에 주로 사용된다.
그림 3 (a) 는 단극성 이진 계단 함수이며, 수학적으로 표현하면 다음과 같다.
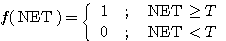 (3)
(3)
여기서, T 는 임계치이다. 식 (3) 과 같은 단극성 계단 함수를 활성화 함수로 사용하면 NET 값이 임계치보다 적을 경우에는 뉴런의 출력이 0 이며, NET 값이 임계치와 같거나 큰 경우에는 뉴런의 출력이 1 이다.
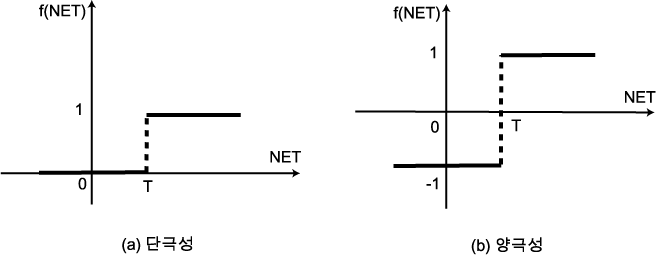
그림 3 계단 함수
그림 3 (b) 는 양극성 이진 계단 함수이며, 수학적으로 표현하면 다음과 같다.
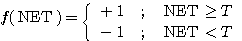 (4)
(4)
여기서, T 는 임계치이다. 식 (4) 와 같은 양극성 계단 함수를 활성화 함수로 사용하면 NET 값이 임계치보다 적을 경우에는 뉴런의 출력이 -1 이며, NET 값이 임계치와 같거나 큰 경우에는 뉴런의 출력은 +1 이다.
예제 3 다음과 같은 신경망 모델에서 그림 3 (a) 와 같은 단극성 계단 함수를 활성화 함수로 사용할 경우, 뉴런의 출력은? 단, 임계치는 2 이다.
입력 벡터 NET = 따라서, 뉴런의 출력은 식 (3) 에 의해,
|
이 결과를 예제 1 과 비교해 보면 동일한 신경망 구조이지만 사용하는 활성화 함수에 따라 뉴런의 출력이 달라짐을 알 수 있다.
4.4 시그모이드 함수
시그모이드 함수 (sigmoid function) 는 그림 4 에 도시한 바와 같이 단극성 또는 양극성 비선형 연속 함수이며, 신경망 모델의 활성화 함수로써 가장 널리 사용되고 있다. 시그모이드 함수는 형태가 S 자 모양이므로 S 형 곡선이라고도 한다.
그림 4 (a) 는 단극성 시그모이드 함수이며, 수학적으로 표현하면 다음과 같다.
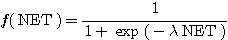 (5)
(5)
여기서, λ 는 경사도이다.
식 (5) 와 같은 단극성 시그모이드 함수를 활성화 함수로 사용하면 뉴런의 출력은 0 에서 1 사이의 값이 되며, 만약 NET=0 이면 뉴런의 출력은 1 / 2 이 된다. 경사도 λ 가 커지면 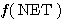 값은 점점
값은 점점 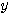 축에 접근하게 되고, 만약 λ → ∞ 이면 시그모이드 함수는 계단 함수와 동일한 형태가 된다.
축에 접근하게 되고, 만약 λ → ∞ 이면 시그모이드 함수는 계단 함수와 동일한 형태가 된다.
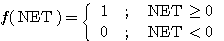
시그모이드 함수는 아날로그 출력이 나오는 장점은 있으나, exp(-λNET) 의 지수 함수 연산을 하여야 하는 문제점이 있다. 이 점을 고려하여 컴퓨터의 계산 시간을 감소시키고 오버플로우 또는 언더플로우의 방지를 위하여 일반적을 경사도 λ = 1 값을 사용한다.
시그모이드 함수의 또 다른 특징은 연속함수이므로 미분 가능하여 델타 학습 방법 등에의 활용이 가능하다는 점이다.
λ = 1 인 경우, 단극성 시그모이드 함수와 그 미분은 식 (6) 과 같다.
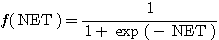 (6)
(6)
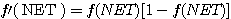
그림 4 (b) 는 양극성 시그모이드 함수이며, 수학적으로 표현하면 다음과 같다.
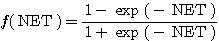 (7)
(7)
양극성 시그모이드 함수도 역시 단극성 시그모이드 함수와 유사한 특성을 가지고 있지만, 식 (7) 과 같은 양극성 시그모이드 함수를 활성화 함수로 사용하면 뉴런의 출력은 -1 에서 +1 사이의 값이 되며, 만약 NET = 0 이면 뉴런의 출력은 0 이다. 양극성 시그모이드 함수의 미분은 다음과 같다.
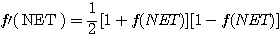 (8)
(8)
시그모이드 함수와 유사한 형태로서 다음과 같은 tanh(x) 함수를 사용하는 경우도 있다.
 (9)
(9)
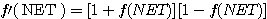
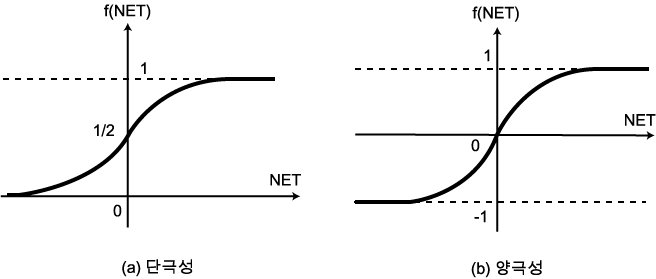
그림 4 시그모이드 함수
예제 4 다음과 같은 신경망 모델에서 단극성 시그모이드 함수를 활성화 함수로 사용할 경우, 뉴런의 출력은? 단, 경사도는 1 이다.
입력 벡터 NET = 따라서, 뉴런의 출력은 식 (6) 에 의해,
|
이 결과에서 보는 바와 같이 시그모이드 함수를 활성화 함수로 사용하면 뉴런의 출력이 아날로그 형태임을 알 수 있다.
5. 신경망의 학습
5.1 학습방법의 분류
인간이 어떤 일을 하기 위해서는 반복 학습이 이루어져야 하듯이 뉴로 컴퓨터도 역시 응용 분야에 활용하기 위해서는 신경망의 학습이 선행되어야 한다. 신경망에서의 학습이라 함은 특정한 응용 목적에 적합하도록 뉴런간의 연결강도를 적응시키는 과정이다. 신경망의 학습 방법은 다음과 같이 크게 3 가지로 구분할 수 있다.
1. 지도 학습 (supervised learning)
2. 자율 학습 (unsupervised learning)
3. 경쟁식 학습 (competitive learning)
지도 학습 방법은 그림 1 (a) 에 도시한 바와 같이 신경망을 학습시키는데 있어서 반드시 입력 x 와 원하는 목표치 d 의 쌍 (x, d) 가 필요하며, 이를 학습 패턴쌍 (training pattern pair) 이라고 한다. 일반적인 학습 절차는 다음과 같다.
1 단계 : 응용 목적에 적합한 신경망 구조를 설계한다.
2 단계 : 연결강도를 초기화한다.
3 단계 : 학습 패턴쌍 (x, d) 를 입력하여 신경망의 출력 y 를 구한다.
4 단계 : 출력 y 와 목표치 d 를 비교하여 그 오차를 산출한다.
5 단계 : 오차를 학습 신호 발생기에 입력하여 연결강도의 변화량 △w 를 계산한다.
6 단계 : 연결강도를 △w 만큼 변경한다.
7 단계 : 변경된 연결강도 (w + △w) 에 대하여 3 단계 ~ 6 단계를 반복한다.
8 단계 : 더 이상 연결강도가 변하지 않으면 학습을 종료한다.
자율 학습 방법은 그림 1 (b) 에 도시한 바와 같이 신경망을 학습시키는데 목표치가 필요없는 방법이며, 일반적인 학습 절차는 다음과 같다.
1 단계 : 응용 목적에 적합한 신경망 구조를 설계한다.
2 단계 : 연결강도를 초기화한다.
3 단계 : 학습 패턴 x 를 입력하여 신경망의 출력 y 를 구한다.
4 단계 : 출력 y 를 학습 신호 발생기에 입력하여 연결강도의 변화량 △w 를 계산한다.
5 단계 : 연결강도를 △w 만큼 변경한다.
6 단계 : 변경된 연결강도 (w + △w) 에 대하여 3 단계 ~ 5 단계를 반복한다.
7 단계 : 더 이상 연결강도가 변하지 않으면 학습을 종료한다.
경쟁식 학습 방법은 그림 1 (a) 의 지도 학습 방법과 동일한 절차이지만, 각 단계에서 전체 연결강도를 변경시키지 않고 단지 특정 부분의 연결강도만을 변화시키는 방법이다. 이 방법은 연결강도를 변화시키는 과정이 축소되므로 신경망의 학습에 소요되는 시간을 상당히 감소시킬 수 있다.
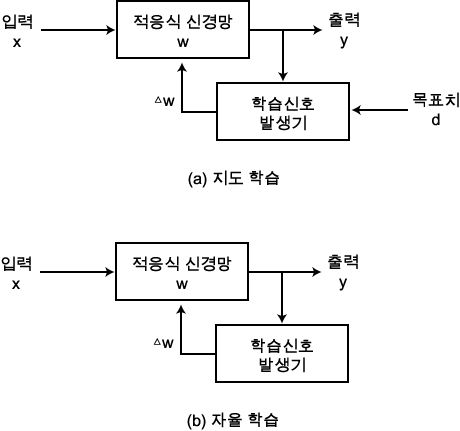
그림 1 신경망의 학습 방법
이미 기술한 바와 같이 신경망의 학습은 연결강도 w 를 변화시키는 과정이며, 일반적으로 연결강도의 변화량 △w 에는 그림 2 에 도시한 바와 같이 학습 신호 (learning signal)  , 학습 입력 패턴 (training input pattern) x, 학습률 (learning rate) α 가 관련되므로
, 학습 입력 패턴 (training input pattern) x, 학습률 (learning rate) α 가 관련되므로  단계 학습과정에서의 연결강도 변화량
단계 학습과정에서의 연결강도 변화량 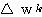 를 다음과 같이 표현할 수 있다.
를 다음과 같이 표현할 수 있다.
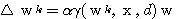 (1)
(1)
따라서, 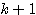 단계 학습과정에서의 연결강도
단계 학습과정에서의 연결강도 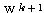 은 다음과 같다.
은 다음과 같다.
 (2)
(2)
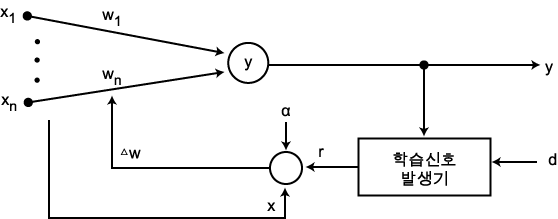
그림 2 연결강도 변경 매카니즘
5.2 Hebb 학습법
Hebb 학습법은 1949 년에 D. Hebb 이 처음 제안하였고, 1988 년 T. McClelland 와 D. Rumelhart 에 의해 확장된 학습 방법으로 순방향 신경망에만 적용될 수 있으며, 이진 또는 연속 활성화 함수가 사용될 수 있다. 초기 연결 강도는 모두 0 에 가까운 작은 값으로 하며, 그림 1 에 도시한 바와 같이 학습 신호로서 출력을 사용하는 점이 특징이다. 따라서, 학습 신호 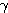 은 다음과 같이 표현할 수 있다.
은 다음과 같이 표현할 수 있다.
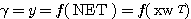 (1)
(1)
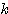 단계에서의 연결강도 변화량
단계에서의 연결강도 변화량 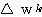 는 신경망의 학습의 식 (1) 에 의해,
는 신경망의 학습의 식 (1) 에 의해,
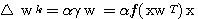 (2)
(2)
따라서, 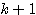 단계에서의 연결강도
단계에서의 연결강도 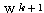 은 다음과 같다.
은 다음과 같다.
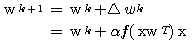 (3)
(3)
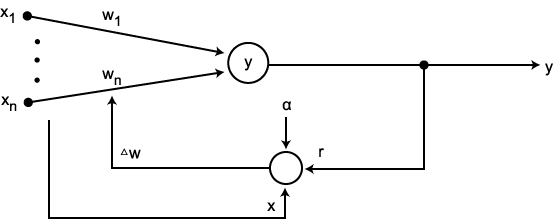
그림 1 Hebb 학습법
예제 1 초기 연결강도가 학습 입력 : (a) 활성화 함수의 그림 3 (a) 의 계단 함수를 활성화 함수 (임계치 T = 0) 로 사용하는 경우 (b) 활성화 함수의 그림 4 (a) 의 시그모이드 함수를 활성화 함수로 사용하는 경우.
(a) 1 단계 : 입력
학습 신호
연결강도의 변화량
따라서,
2 단계 : 입력
따라서,
3 단계 : 입력
(b) 1 단계 : 입력
학습 신호
연결강도의 변화량
따라서,
2 단계 : 입력
따라서,
3 단계 : 입력
|
5.3 퍼셉트론 학습법
퍼셉트론 학습법 (Perceptron Learning) 은 1958년 F. Rosenblatt 가 제안한 학습 방법으로 이진 또는 연속 활성화 함수가 사용될 수 있다. 초기 연결강도는 임의의 값으로 할 수 있으며, 그림 1 에 도시한 바와 같이 학습 신호로써 목표치 d 와 실제 출력 y 의 차이 즉, 오차를 사용하는 점이 특징이다. 따라서, 학습신호 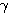 은 다음과 같이 구할 수 있다.
은 다음과 같이 구할 수 있다.
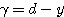 (1)
(1)
k 단계에서의 연결강도 변화량 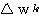 는 신경망의 학습에서 식 (1) 에 의해,
는 신경망의 학습에서 식 (1) 에 의해,
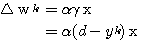 (2)
(2)
따라서, 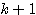 단계의 연결강도
단계의 연결강도 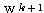 은 다음과 같다.
은 다음과 같다.
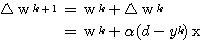 (3)
(3)
한편, 퍼셉트론 학습법에서는 일반적으로 활성화 함수의 그림 3 (b) 와 같은 양극성 계단 함수를 주로 사용하므로, 식 (2) 는 다음과 같이 간략화될 수 있다.
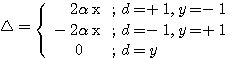 (4)
(4)
식 (4)에서 알 수 있듯이 만약, 목표치가 +1 일 때 실제 출력이 -1 이면, 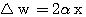 만큼 연결강도를 감소시켜서 뉴런의 입력 가중합이 적어지게 함으로써 원하는 결과를 얻도록 하고 있다.
만큼 연결강도를 감소시켜서 뉴런의 입력 가중합이 적어지게 함으로써 원하는 결과를 얻도록 하고 있다.
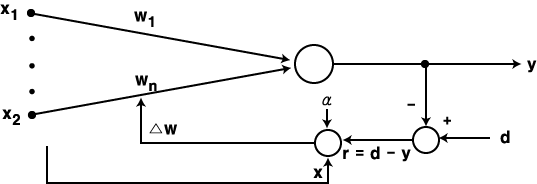
그림 1 퍼셉트론 학습법
예제 1 Hebb 학습법의 예제 1 과 동일한 조건의 신경망을 퍼셉트론 학습법으로 학습시킬 때 연결강도의 변화 과정은? 단, 1 단계 : 입력
학습 신호
따라서,
입력 2 단계 : 입력
따라서,
3 단계 : 입력
|
5.4 델타 학습법
델타 학습법 (Delta Learning) 은 1986 년 T. McClelland 와 D. Rumelhart 가 제안한 학습 방법으로 연속 활성화 함수만을 사용한다. 그림 1 에 도시한 바와 같이 학습 신호로서 목표치 d 와 실제 출력 y 의 차이 뿐만 아니라 활성화 함수의 미분값이 사용되는 점이 특징이다. 따라서, 학습 신호 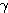 은 다음과 같이 구할 수 있다.
은 다음과 같이 구할 수 있다.
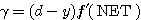 (1)
(1)
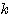 단계에서의 연결강도 변화량
단계에서의 연결강도 변화량 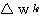 는 신경망의 학습의 식 (1) 에 의해
는 신경망의 학습의 식 (1) 에 의해
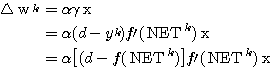 (2)
(2)
따라서, 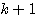 단계의 연결강도
단계의 연결강도 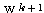 은 다음과 같다.
은 다음과 같다.
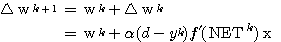 (3)
(3)
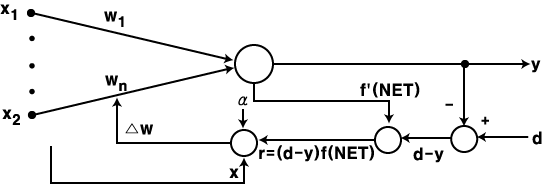
그림 1 델타 학습법
예제 1 퍼셉트론 학습법의 예제 1 과 동일한 조건의 신경망을 델타 학습법으로 학습시킬 때 연결강도의 변화 과정은? 단, 활성화 함수로는 활성화 함수의 그림 4 (a) 의 단극성 시그모이드 함수 1 단계 : 입력
식 활성화 함수의 식 (6) 에 의해
학습 신호
연결강도 변화량
2 단계 : 입력
따라서, 식 (2), (3) 에 의해
3 단계 : 입력
|
5.5 LMS 학습법
LMS (Least Mean Square) 학습법은 1962 년 B. Widrow 가 제안한 방법으로 항등 함수를 활성화 함수로 사용한다. 초기 연결강도는 임의의 값으로 하며, 그림 1 에 도시한 바와 같이 학습 신호로써 목표치 d 와 실제 출력 y 의 차이가 사용되는 점이 특징이다. 따라서, 학습 신호 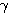 은 다음과 같이 표현할 수 있다.
은 다음과 같이 표현할 수 있다.
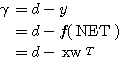 (1)
(1)
k 단계에서의 연결강도 변화량 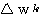 는 신경망의 학습의 식 (1) 에 의해
는 신경망의 학습의 식 (1) 에 의해
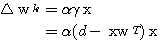 (2)
(2)
따라서, 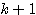 단계의 연결강도
단계의 연결강도 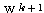 은 다음과 같다.
은 다음과 같다.
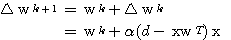 (3)
(3)
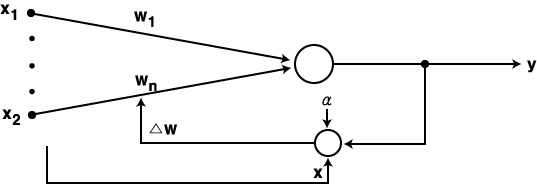
그림 1 LMS 학습법
예제 1 Hebb 학습법의 예제 1 과 동일한 조건의 신경망을 LMS 학습법으로 학습시킬 때 연결강도의 변화 과정은? 단, 항등 함수를 활성화 함수로 사용한다. 1 단계 : 입력
학습 신호
2 단계 : 입력
따라서,
3 단계 : 입력
|
5.6 경쟁식 학습법
주로 사용되는 경쟁식 학습법 (Competitive Learning) 에는 1987 년 R. Hecht-Nielsen 이 제안한 instar 학습법과 1974 년 S. Grossberg 가 제안한 outstar 학습법 등이 있다.
instar 학습법은 경쟁식 신경망에 사용되며, 그림 1 (a) 에 도시한 바와 같이 학습 과정에서 winner 뉴런  와 관련된 연결강도
와 관련된 연결강도  만을 변경하는 학습 방법이며, 연결강도의 변화량
만을 변경하는 학습 방법이며, 연결강도의 변화량  는 다음과 같다.
는 다음과 같다.
반면에, outstar 학습법은 경쟁식 신경망에 사용되며, 그림 1 (b) 에 도시한 바와 같이 학습 과정에서 winner 뉴런 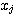 와 관련된 연결강도
와 관련된 연결강도 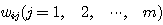 만을 변경하는 학습 방법이며, 연결강도의 변화량
만을 변경하는 학습 방법이며, 연결강도의 변화량 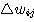 는 다음과 같다.
는 다음과 같다.
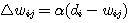 (1)
(1)
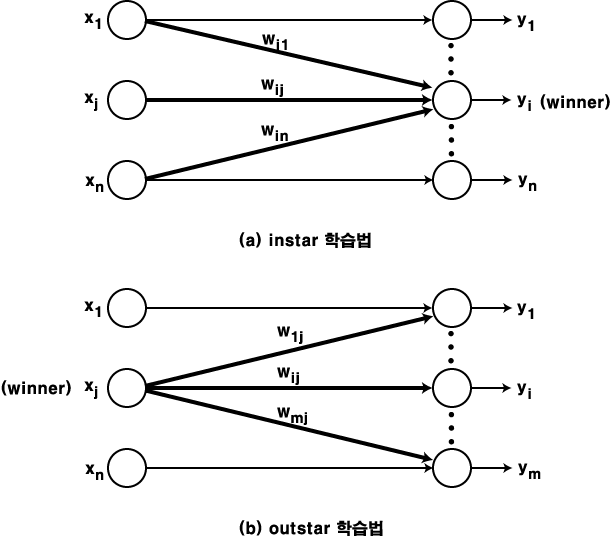
그림 1 경쟁식 학습법
지금까지 언급한 여러 가지 학습 방법의 특징을 표 1 에 비교하였다.
표 1 학습법의 특징 비교
학습법 | 초기 연결강도 | 연결강도 변화량 |
Hebb | 적은 값 |
|
퍼셉트론 | 임의 값 |
|
델타 | 임의 값 |
|
LMS | 임의 값 |
|
instar | 임의 값 |
|
outstar | 0 |
|
6. 표기법
본 절에서는 독자들의 이해를 돕기 위하여 신경망 모델에 일반적으로 사용되는 기호들을 정의하였다.
| 입력층의 입력 벡터 출력층의 출력층의 출력 벡터 은닉층의 입력층의 입력층 (은닉층) 의 연결강도 벡터 또는 매트릭스
연결강도의 변화량 학습률 학습 신호 오차 신호 활성화 함수 뉴런의 입력 가중합 뉴런 바이어스 목표치 임계치 벡터 해밍거리 |
출처 : http://www.aistudy.com/neural/theory_oh.htm#_bookmark_2361618
'패턴인식 & 기계학습' 카테고리의 다른 글
| SVM(Support Vector Machine) (0) | 2014.11.04 |
|---|---|
| Heap theory(헵 이론) (0) | 2014.11.04 |
| Boltzmann machine(볼츠만 머신) (0) | 2014.11.04 |
| 결정 트리 분기 (0) | 2014.10.25 |
| 다층 퍼셉트론 (2) | 2014.10.24 |
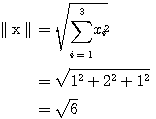
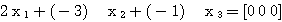
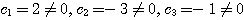 이므로 선형 독립이 아니다.
이므로 선형 독립이 아니다.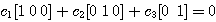 을 만족하는 모두 0 이 아닌 어떠한
을 만족하는 모두 0 이 아닌 어떠한 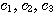 도 존재하지 않으므로 선형 독립이다.
도 존재하지 않으므로 선형 독립이다.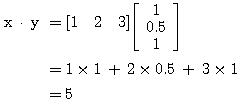
 와
와  는 서로 직교하는가?
는 서로 직교하는가? 와
와 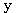 의 내적은 식 (4) 에 의하여
의 내적은 식 (4) 에 의하여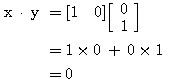
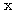 와
와 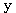 는 서로 직교한다.
는 서로 직교한다.
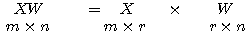
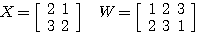
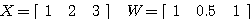
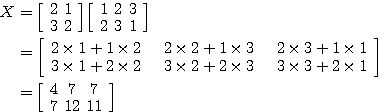
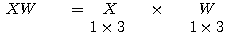
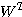 를 취하면 곱할 수 있다.
를 취하면 곱할 수 있다.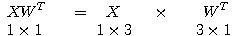
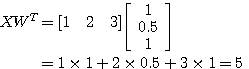
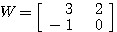 의 고유값은?
의 고유값은?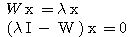
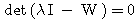
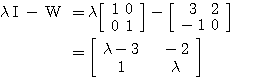
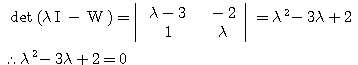
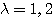 이다.
이다.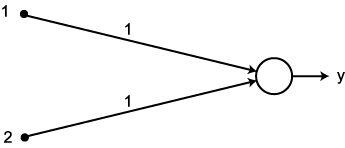
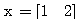 , 연결 강도
, 연결 강도 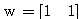 이므로, 뉴런의 입력 가중합 NET 는 다음과 같다.
이므로, 뉴런의 입력 가중합 NET 는 다음과 같다.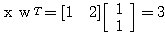
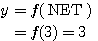
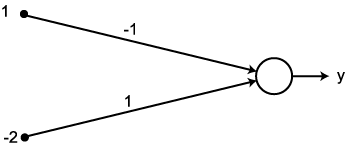
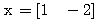 , 연결 강도
, 연결 강도 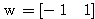 이므로, 뉴런의 입력 가중합 NET 는 다음과 같다.
이므로, 뉴런의 입력 가중합 NET 는 다음과 같다.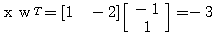
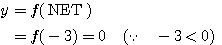
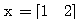 , 연결 강도
, 연결 강도 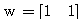 이므로,
이므로,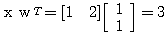
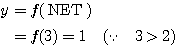
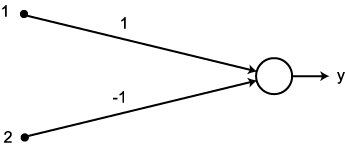
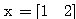 , 연결 강도
, 연결 강도 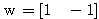 이므로,
이므로,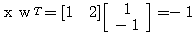
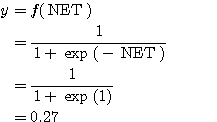
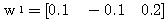 인 신경망을 Hebb 학습법으로 학습시킬 때 연결강도의 변화 과정은? 단, 학습률
인 신경망을 Hebb 학습법으로 학습시킬 때 연결강도의 변화 과정은? 단, 학습률 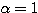 이다.
이다.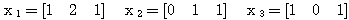

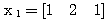 에 대한 뉴런의
에 대한 뉴런의 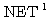 값은,
값은,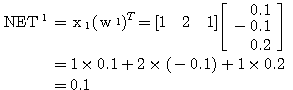
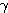 은 식 (1), 활성화 함수에서 식 (3) 에 의해,
은 식 (1), 활성화 함수에서 식 (3) 에 의해,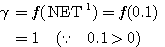
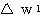 은 식 (2) 에 의해,
은 식 (2) 에 의해,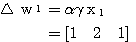
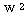 는 식 (3) 에 의해,
는 식 (3) 에 의해,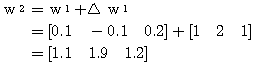
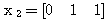 에 대하여 1 단계와 마찬가지로
에 대하여 1 단계와 마찬가지로 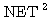 ,
, 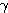 을 구할 수 있다.
을 구할 수 있다.
 ,
,  은 다음과 같다.
은 다음과 같다.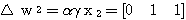
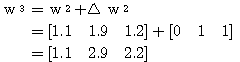
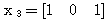 에 대하여도 동일하게
에 대하여도 동일하게 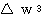 ,
, 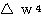 를 구할 수 있다.
를 구할 수 있다.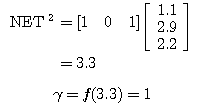
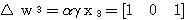
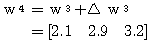
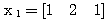 에 대한 뉴런의
에 대한 뉴런의  값은,
값은,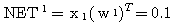
 은 식 (1), 활성화 함수에서 식 (6) 에 의해,
은 식 (1), 활성화 함수에서 식 (6) 에 의해,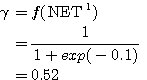
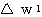 은 식 (2) 에 의해,
은 식 (2) 에 의해,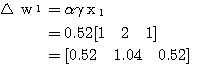
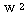 는 식 (3) 에 의해,
는 식 (3) 에 의해,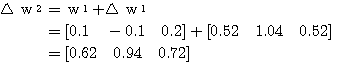
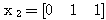 에 대하여 1 단계와 마찬가지로
에 대하여 1 단계와 마찬가지로 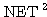 ,
, 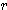 을 구할 수 있다.
을 구할 수 있다.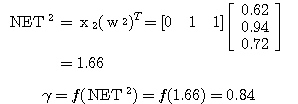
 은 다음과 같다.
은 다음과 같다.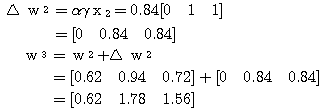
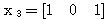 에 대하여도 동일하게
에 대하여도 동일하게 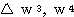 를 구할 수 있다.
를 구할 수 있다.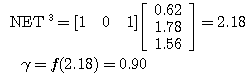
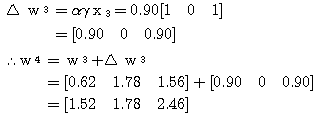
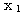 이 입력될 경우에는 목표치가 +1,
이 입력될 경우에는 목표치가 +1, 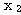 와
와 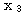 가 입력될 경우에는 목표치가 -1 이 되도록 한다. 또한, 활성화 함수로 그림 3 (b) 의 양극성 계단 함수 (임계치 T = 0) 를 사용한다.
가 입력될 경우에는 목표치가 -1 이 되도록 한다. 또한, 활성화 함수로 그림 3 (b) 의 양극성 계단 함수 (임계치 T = 0) 를 사용한다.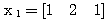 에 대한 뉴런의
에 대한 뉴런의 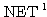 과
과 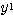 값은,
값은,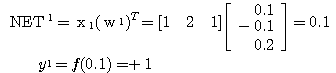
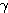 은 식 (1) 에 의해,
은 식 (1) 에 의해,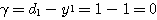
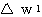 과
과 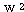 는 식 (2), (3) 에 의해,
는 식 (2), (3) 에 의해,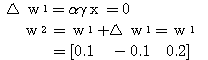
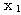 에 대한 출력
에 대한 출력 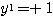 과 목표치
과 목표치 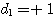 이 동일하므로 연결강도를 변화시키지 않음을 알 수 있다.
이 동일하므로 연결강도를 변화시키지 않음을 알 수 있다.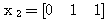 에 대하여 1 단계와 마찬가지로
에 대하여 1 단계와 마찬가지로 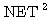 ,
, 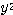 를 구할 수 있다.
를 구할 수 있다.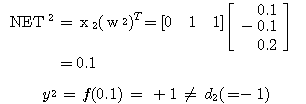
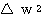 ,
, 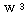 은 다음과 같다.
은 다음과 같다.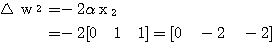
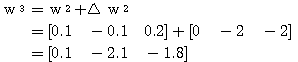
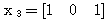 에 대하여도 동일하게
에 대하여도 동일하게 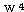 를 구할 수 있다.
를 구할 수 있다.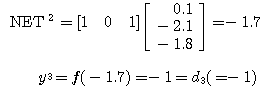
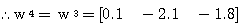
 을 사용한다.
을 사용한다.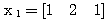 에 대한 뉴런의
에 대한 뉴런의 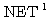 과
과 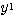 값은,
값은,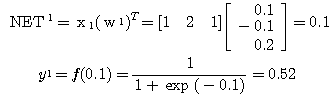
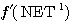 는,
는,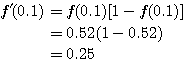
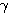 은 식 (1) 에 의해,
은 식 (1) 에 의해,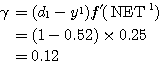
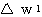 는 식 (2) 에 의해,
는 식 (2) 에 의해,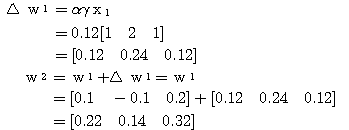
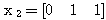 에 대하여 1 단계와 마찬가지로
에 대하여 1 단계와 마찬가지로 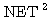 ,
, 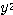 ,
, 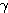 를 구할 수 있다.
를 구할 수 있다.
 ,
,  은 다음과 같다.
은 다음과 같다.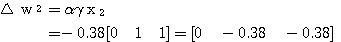
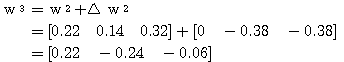
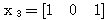 에 대하여도 동일하게
에 대하여도 동일하게 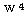 를 구할 수 있다.
를 구할 수 있다.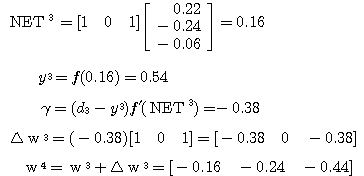
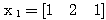 에 대한 뉴런의
에 대한 뉴런의 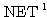 과
과 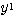 값은,
값은,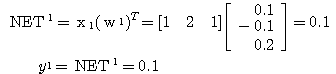
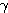 은 식 (1) 에 의해,
은 식 (1) 에 의해,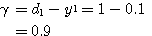
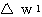 과
과 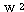 는 식 (2), (3) 에 의해,
는 식 (2), (3) 에 의해,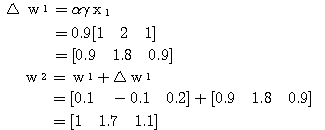
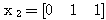 에 대하여 1 단계와 마찬가지로
에 대하여 1 단계와 마찬가지로 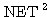 ,
, 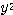 ,
, 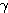 를 구할 수 있다.
를 구할 수 있다.
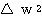 ,
, 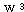 는 식 (2), (3) 에 의해,
는 식 (2), (3) 에 의해,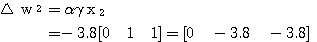
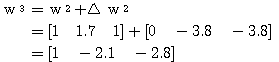
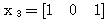 에 대하여도 동일하게
에 대하여도 동일하게 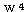 를 구할 수 있다.
를 구할 수 있다.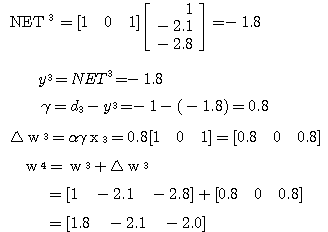
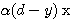
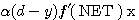
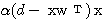
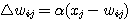
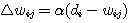
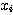
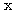
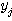
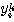
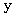
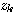
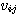
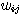
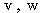
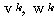
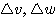
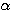
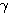
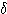
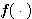
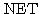
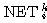
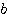
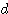
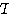
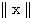
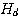
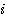 번째 뉴런
번째 뉴런 번째 뉴런 또는 출력
번째 뉴런 또는 출력 번째 뉴런의
번째 뉴런의 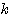 단계에서의 출력
단계에서의 출력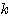 번째 뉴런
번째 뉴런 번째 뉴런과 은닉층의
번째 뉴런과 은닉층의 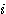 번째 뉴런간의 연결강도
번째 뉴런간의 연결강도 번째 뉴런과 출력층의
번째 뉴런과 출력층의 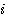 번째 뉴런간의 연결강도
번째 뉴런간의 연결강도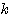 학습 단계에서의 연결강도
학습 단계에서의 연결강도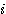 의
의 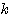 단계에서의 입력 가중합
단계에서의 입력 가중합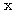 의 norm
의 norm